Published on

Java로 구현하는 GCD, LCM: 최대공약수와 최소공배수

Authors
  • avatar
    Name
    Kil Hyeon Jun
    Twitter

Java로 구현하는 GCD, LCM: 최대공약수와 최소공배수

최대공약수(GCD: Greatest Common Divisor)와 최소공배수(LCM: Least Common Multiple)는 수학과 컴퓨터 과학에서 중요한 개념이다.
이 글에서는 Java를 사용하여 이 두 가지 알고리즘을 구현하는 방법을 알아본다.

최대공약수 (GCD)

최대공약수는 두 수 또는 그 이상의 정수의 공통된 약수 중 가장 큰 수를 말한다.
GCD를 구하는 가장 효율적인 방법 중 하나는 유클리드 알고리즘을 사용하는 것이다.

유클리드 알고리즘 (유클리드 호제법)

유클리드 알고리즘의 기본 원리는 다음과 같다.

두 양의 정수 a와 b에 대해 (a > b), a를 b로 나눈 나머지를 r이라고 하면,
gcd(a, b) = gcd(b, r)이다.
이 과정을 r이 0이 될 때까지 반복한다.

다음은 유클리드 호제법의 과정을 사각형으로 시각화한 그림이다.

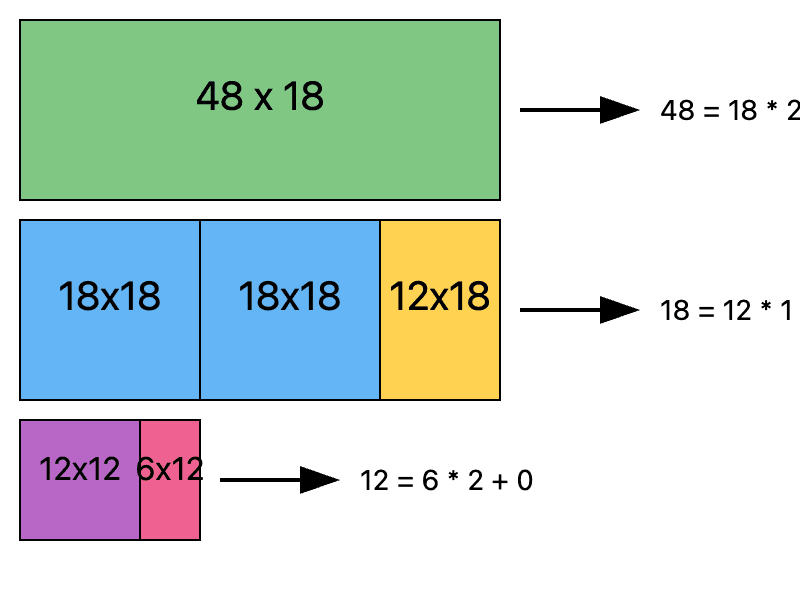
사각형으로 표현한 유클리드 호제법

이 그림은 48과 18의 최대공약수를 구하는 과정을 보여준다:

  1. 첫 번째 단계: 48x18 크기의 사각형으로 시작한다.
  2. 두 번째 단계: 18x18 크기의 사각형 2개와 12x18 크기의 사각형 1개로 나눈다. (48 = 18 * 2 + 12)
  3. 세 번째 단계: 12x12 크기의 사각형 1개와 6x12 크기의 사각형 1개로 나눈다. (18 = 12 * 1 + 6)
  4. 마지막 단계: 12를 6으로 나누면 나머지가 0이 된다. (12 = 6 * 2 + 0)

따라서 최대공약수는 6이다.

이 과정을 Java로 구현한 GCD 함수는 다음과 같다.

반복적 구현

public static int gcd(int a, int b) {
    while (b != 0) {
        int temp = b;
        b = a % b;
        a = temp;
    }
    return a;
}

재귀적 구현

유클리드 알고리즘은 재귀적 특성을 가지고 있어 재귀 함수로도 간단히 표현할 수 있다.

public static int gcdRecursive(int a, int b) {
    if (b == 0) {
        return a;
    }
    return gcdRecursive(b, a % b);
}

이 재귀 구현은 다음과 같이 작동한다.

  1. 기본 케이스(base case): b가 0이면, a가 GCD이다.
  2. 재귀 케이스(recursive case): b가 0이 아니면, gcdRecursive(b, a % b)를 호출한다.

재귀 구현은 알고리즘의 본질을 직관적으로 표현하며 수학적 정의와 더 가깝게 대응된다.
하지만 입력값이 매우 큰 경우 스택 오버플로우가 발생할 수 있으므로 주의해야 한다.

최소공배수 (LCM)

최소공배수는 두 수 또는 그 이상의 정수의 공통된 배수 중 가장 작은 수를 말한다.
LCM은 GCD를 이용하여 쉽게 계산할 수 있다.

두 수 a와 b의 LCM은 다음 공식으로 구할 수 있다.

최대 공약수와 최소 공배수의 곱은 두수의 곱과 같기에 a * b = GCD(a, b) * LCM(a, b)
따라서 LCM(a, b) = (a * b) / GCD(a, b) 이다.

Java로 구현한 LCM 함수는 다음과 같다.

public static int lcm(int a, int b) {
    return Math.abs(a * b) / gcd(a, b);
}

사용 예제

이제 위에서 구현한 GCD와 LCM 함수를 사용하는 예제를 살펴보자.

public static void main(String[] args) {
    int a = 48;
    int b = 18;

    System.out.println("GCD of " + a + " and " + b + " is: " + gcd(a, b));
    System.out.println("Recursive GCD of " + a + " and " + b + " is: " + gcdRecursive(a, b));
    System.out.println("LCM of " + a + " and " + b + " is: " + lcm(a, b));
}

이 코드를 실행하면 다음과 같은 결과가 출력된다.

GCD of 48 and 18 is: 6
Recursive GCD of 48 and 18 is: 6
LCM of 48 and 18 is: 144

결론

GCD와 LCM은 수학적 계산뿐만 아니라 알고리즘 최적화, 암호학 등 다양한 분야에서 사용된다. Java로 이러한 기본적인 수학 개념을 구현함으로써, 더 복잡한 알고리즘과 응용 프로그램을 개발할 수 있는 기초를 다지게 된다.

이 글에서 소개한 방법들은 간단하면서도 효율적인 구현 방식이다. 반복적 방법과 재귀적 방법 모두 유용하며, 상황에 따라 적절한 방법을 선택하면 된다. 실제 프로젝트에서는 Java의 BigInteger 클래스를 사용하여 더 큰 숫자들도 처리할 수 있도록 하는 것이 좋다.

유클리드 호제법을 사각형으로 시각화한 그림을 통해 알고리즘의 작동 원리를 직관적으로 이해할 수 있다. 이러한 시각화는 복잡한 알고리즘을 이해하고 구현하는 데 큰 도움이 된다.

계속해서 알고리즘을 공부하고 구현해 보면서, 프로그래밍 실력을 향상시켜 나가자!

Discuss on Twitter • View on GitHub